¿Cómo elegir la forma de curva de leva de las lentes con zoom?
En la etapa final del diseño de la lente zoom, es necesario diseñar la curva de la leva. Para equilibrar la uniformidad del cambio de ampliación de la imagen y el ángulo de rotación de la leva, se debe seleccionar una forma de curva de leva adecuada y se debe establecer una cierta relación funcional entre la ampliación de la imagen M y el ángulo de rotación de la leva θ.
De acuerdo con las condiciones de contorno reales y la continuidad de la función que debe cumplir la curva de leva, se establecen varias relaciones funcionales comunes entre M y θ, y Matlab simula los ejemplos de diseño.
Los resultados muestran que cuando la relación de función de potencia establecida entre el aumento de imagen M y el ángulo de rotación de la leva θ y el ángulo de aumento de presión no excede el valor permitido, el equilibrio de cambio de aumento variable es el mejor, la curva de cambio de aumento es suave y no hay punto de inflexión de la leva. Este método puede facilitar a los diseñadores cambiar la forma de la curva de leva de acuerdo con los diferentes requisitos de diseño y encontrar la mejor curva de leva de zoom.
En el sistema de zoom, la cámara es el componente que controla el movimiento del grupo de lentes y permite que el sistema cambie la distancia focal mientras mantiene estable el plano de la imagen. La operación de zoom suave, flexible y rápida es un contenido importante del rendimiento del zoom, que está directamente relacionado con la rugosidad del perfil de la leva y el ángulo de presión de la curva de la leva.
Si la curva de leva tiene un ángulo de inclinación mayor en una determinada sección, parece más pronunciada. En el proceso de girar la leva, habrá una sensación más pesada en la mano. El engranaje que hace girar la leva está desgastado y el borde de la ranura de la leva puede incluso apretarse y deformarse, lo que afecta la calidad de la imagen; cuando es más grave, la cámara se atasca y no se puede utilizar en absoluto.
En la lente de zoom compensada mecánicamente, al seleccionar la relación de movimiento entre el movimiento del grupo de zoom y el ángulo de la leva, se puede satisfacer que la ampliación de la imagen cambie a una velocidad uniforme o con una aceleración uniforme durante el proceso de zoom. Esto es muy prometedor ya sea para televisión, fotografía cinematográfica o lentes con zoom utilizados en seguimiento militar.
Pero al mismo tiempo, el ángulo de presión correspondiente a la curva de leva en ambos extremos de las distancias focales larga y corta será muy grande. Cuando se busca la miniaturización de la lente de zoom, el par de rotación de la leva a menudo excederá el valor tolerable. Por lo tanto, es necesario elegir la forma de la curva de la leva y encontrar un equilibrio entre la uniformidad del cambio de ampliación de la imagen y el ángulo de rotación de la leva.
Este artículo establece la relación de la función de potencia entre la ampliación de la imagen M y el ángulo de rotación de la leva θ. Combinada con la ecuación del sistema de zoom, la interfaz de simulación de Matlab está escrita para simular la forma de la curva de leva. Los resultados muestran que la función establecida M-θ es más lineal que el ajuste de curva tradicional y el método θ-x, la curva de leva es más suave, el ángulo de aumento de presión es menor en general (<45°) y el cambio de aumento es más equilibrado. .
La teoría básica del sistema de zoom.
La etapa final del diseño de la lente con zoom, es decir, después de determinar los parámetros del mecanismo óptico (radio, intervalo, material de vidrio) de cada elemento de la lente, también es necesario calcular la relación numérica entre el desplazamiento del grupo de zoom y la compensación. grupo para procesar la pista de leva. A continuación analizamos las dos formas de la ecuación de la curva de leva.
Forma 1: Obtenga la cantidad de movimiento del grupo de compensación y a partir de la cantidad de movimiento del grupo de aumento variable x, y luego obtenga la curva de leva de aumento variable, es decir
x→y→m2* ,metro3* →M (1)
Forma 2: Obtenga los aumentos m2* y m3* del grupo de aumento variable y el grupo de compensación del aumento variable M requerido por el sistema, y obtenga el movimiento x, y del grupo de aumento variable y el grupo de compensación, y luego obtenga la curva de leva, es decir
M→m2*,metro3*→x,y (2)
De las dos formas anteriores se puede ver que para establecer la ecuación de la leva y luego procesar la pista de la leva, es necesario establecer la relación funcional entre el ángulo de la leva y una de las variables anteriores.
Diseño de curva de cámara de zoom.
Para equilibrar la uniformidad del cambio de ampliación de la imagen y el ángulo de la leva, es necesario seleccionar una forma de curva de leva adecuada. Esto requiere que establezcamos una cierta relación funcional entre la ampliación de la imagen M y el ángulo de rotación de la leva θ, que se discutirá a continuación.
1. Discusión formal
Primero, especifique los siguientes símbolos.
F1,F2,F3,F4: Son las distancias focales del grupo fijo frontal, el grupo de zoom, el grupo de compensación y el grupo fijo trasero;
metro2,metro3: respectivamente, la ampliación lateral del grupo de zoom y el grupo de compensación;
metro23= metro2metro3: El aumento lateral de la parte de aumento variable compuesta por el grupo de aumento variable y el grupo de compensación;
metro230:El aumento horizontal de la parte de aumento variable en el punto inicial (θ=0) en la posición focal. Este ejemplo es la posición de distancia focal más corta;
L: El movimiento máximo del grupo de zoom;
θ: El ángulo de rotación de la leva;
α: El ángulo máximo de rotación de la leva;
R: Radio del tambor:
M: ampliación de zoom;
Max: Ampliación máxima del zoom;
x,y: representan respectivamente la cantidad de movimiento del grupo de zoom y el grupo de compensación;
Entre ellos, kXy kyson las pendientes del grupo de zoom de la curva de leva y del grupo de compensación respectivamente, es decir, el valor tangente de su ángulo de aumento de presión.
Al construir la relación funcional entre θ y M, se deben prestar atención a dos condiciones de contorno:
Condición de frontera uno: cuando θ=0°, M=1
Condición de frontera dos: Cuando θ=α, M=Mmax
(1) θ tiene una relación lineal con M
Puede hacer que el cambio de aumento produzca un efecto uniforme, esta relación se puede expresar como
La fórmula anterior se puede utilizar para diferenciar θ y obtener la tasa de cambio de aumento:
(1) Existe una relación lineal entre θ y M
(a) Primero construya la relación de función de potencia entre θ y M:
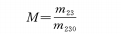
M: ampliación de zoom;
METROmáximo: Ampliación máxima del zoom;
x,y: representan respectivamente la cantidad de movimiento del grupo de zoom y el grupo de compensación;
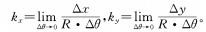
Entre ellos, kXy kyson las pendientes del grupo de zoom de la curva de leva y del grupo de compensación respectivamente, es decir, el valor tangente de su ángulo de aumento de presión.
Al construir la relación funcional entre θ y M, se deben prestar atención a dos condiciones de contorno:
Condición de frontera uno: cuando θ=0°, M=1
Condición de frontera dos: Cuando θ=α, M=Mmax
(1) θ tiene una relación lineal con M
Puede hacer que el cambio de aumento produzca un efecto uniforme, esta relación se puede expresar como

La fórmula anterior se puede utilizar para diferenciar θ y obtener la tasa de cambio de aumento:
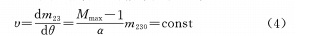
(1) Existe una relación lineal entre θ y M
(a) Primero construya la relación de función de potencia entre θ y M:

En la fórmula, M, Mmáximo, α, θ se definen como anteriormente, n es el coeficiente de la curva de leva, que también puede considerarse como un coeficiente de ajuste, y se especifica n≠0. (5) Diferenciando la fórmula a θ se puede obtener:
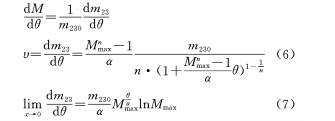
(b) Construya la relación de función exponencial entre θ y M
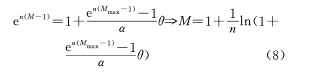
La fórmula (8) se puede obtener diferenciando θ:
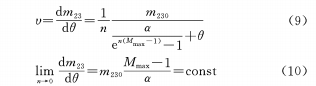
(c) Construya la relación de función logarítmica entre θ y M
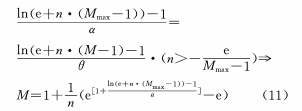
Después de la diferenciación, hay
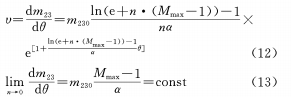
(d) Construya la relación de la función gaussiana entre θ y M
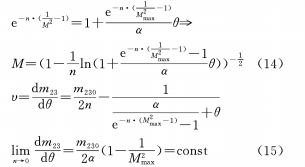
(e) Las cuatro relaciones funcionales anteriores se utilizan en el caso de n≠0. Para el caso de n=0, estipulamos:

Es decir, existe una relación lineal entre θ y x, que es la relación más utilizada actualmente. Diferenciar la ecuación (16) y la ecuación de leva para obtener la tasa de cambio de la ampliación como
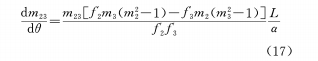
Los resultados anteriores se analizan a continuación.
(1) Cuando θ tiene una relación lineal con M, se puede ver en la fórmula (4) que los tiempos variables del sistema y la velocidad uniforme son muy deseables. Sin embargo, debido a la relación no lineal entre la cantidad de movimiento x del grupo de zoom y M, inevitablemente conducirá a la no uniformidad de la velocidad de movimiento del grupo de lentes y al desequilibrio del ángulo de presión.
(2) Cuando θ y M están en una relación no lineal, y θ y M están en una relación de función de respaldo, si n es constante, la ampliación variable y el ángulo de rotación cambiarán en una relación de función de respaldo. Se puede ver en la fórmula (7) que cuando el coeficiente de la curva de la leva n se acerca a 0, el aumento variable y el ángulo de rotación cambian exponencialmente, es decir, el aumento aumenta cada vez más rápido durante la rotación de la leva.
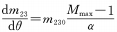
Cuando n=1 y aparecen las condiciones de la fórmula anterior, la tasa de cambio de aumento es un valor fijo, es decir, durante toda la rotación de la leva desde el final de la distancia focal más corta hasta el final de la distancia focal más larga. , el cambio de aumento es uniforme, lo que se convierte en la situación analizada en la fórmula (4).
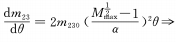
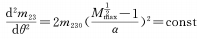
Cuando m = 1/2 y aparecen las condiciones de la fórmula anterior, el cambio de aumento se acelera uniformemente, que también es lo que esperamos.
(3) La relación entre θ y M es exponencial, logarítmica y gaussiana. Cuando n es constante, la tasa de cambio de aumento es inversamente proporcional a θ, es decir, cuando la leva gira gradualmente desde la distancia focal más corta a la distancia focal más larga, la tasa de cambio de aumento se vuelve cada vez más lenta.
Cuando n cambia, la tasa de cambio de aumento no es lineal con la curva θ. Cuando el coeficiente de la curva de leva n se aproxima a 0, la tasa de cambio del aumento es constante, es decir, el cambio del aumento es lineal.
En términos generales, el principio de selección de la curva de leva es seleccionar la forma de curva con el mejor cambio de aumento variable y una curva de cambio de aumento suave cuando el ángulo de aumento de presión no excede el valor permitido.
A través de la discusión anterior y la simulación experimental de Matlab, entendemos que cuando la relación entre θ y M es una función de respaldo, al seleccionar el coeficiente de ajuste apropiado n, se puede lograr que cuando el ángulo de presión esté cerca del valor permitido, la variable El cambio de aumento tiene el mejor equilibrio y el cambio de aumento. La curva es suave y no hay punto de inflexión de la leva.
Sin embargo, ninguna de las otras funciones puede lograr mejores resultados. La Figura 1 es un diagrama de simulación de leva diseñado utilizando un software de dibujo tridimensional basado en los resultados del análisis anterior. A continuación se describen los resultados de nuestros experimentos de simulación.
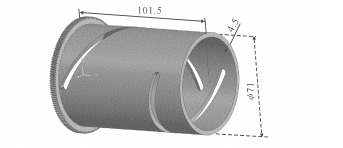
Fig.1 Figura de simulación de leva.
2. Análisis y simulación
Combine las dos formas de métodos de resolución de curvas de leva proporcionadas anteriormente y la relación funcional entre θ y M para compilar la interfaz GUI de Matlab.
Los parámetros de entrada del programa son:
Coeficiente de curva de leva n, distancia focal corta f del sistema óptico0, longitud focal del grupo de aumento variable f2, longitud focal del grupo de compensación f3, plomo (distancia de movimiento del grupo de aumento variable desde una distancia focal corta a una distancia focal larga) wl, objetos en el grupo de aumento variable en una distancia focal corta, la distancia es l20, la distancia de imagen del grupo de compensación es ll30en enfoque corto, el ángulo máximo de rotación de la leva α, el intervalo del ángulo de rotación mu en unidades de ángulo y el diámetro del tambor de la leva dd.
Los parámetros de salida del programa son:
Ángulo de rotación, movimiento del grupo de zoom, movimiento del grupo de compensación, distancia focal, ángulo de aumento de presión del grupo de zoom, ángulo de aumento de presión del grupo de compensación y datos y gráficos de relación de zoom.
A través de esta interfaz del programa, puede ver fácilmente la relación entre la relación de zoom y el ángulo de rotación, observar si el ángulo de aumento de presión excede el valor permitido y cambiar el coeficiente de ajuste para cambiar rápidamente la relación anterior y encontrar la mejor curva de leva requerida. .
toma el 20XSistema de compensación positiva de zoom continuo diseñado por el grupo de investigación como ejemplo para seleccionar la curva de leva.
Los parámetros fijos son:
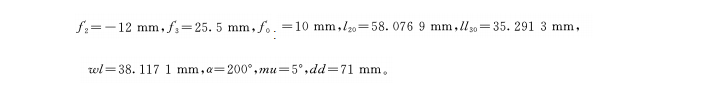
Parámetro variable: coeficiente de ajuste n
Este programa es editable para todos los parámetros anteriores. Para facilitar la discusión, aquí consideramos principalmente la influencia del coeficiente de ajuste n en el resultado.
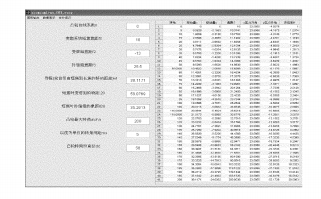
Fig. 2 Interfaz de simulación de Matlab
(1) Cuando n = 0, existe una relación lineal entre θ y x, como se muestra en la Figura 3.
(2) Cuando n = 0,047, el gráfico de la función de potencia se muestra en la Figura 4.
(3) Cuando n= 0.000 1, la gráfica de la función exponencial se muestra en la Figura 5.
(4) Cuando n = 2,32, el gráfico de la función logarítmica se muestra en la Figura 6.
(5) Cuando n = 0,1, la gráfica de la función gaussiana se muestra en la Figura 7.
El experimento demuestra que la discusión anterior sobre la relación de varias funciones es consistente con la tendencia de la curva gráfica.
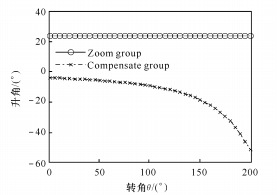
(a) Relación entre el ángulo de aumento de presión y el ángulo de rotación
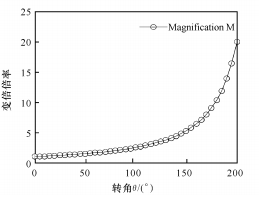
(b) Relación entre la relación de zoom y el ángulo de rotación
Fig. 3 Relación lineal entre θ y x
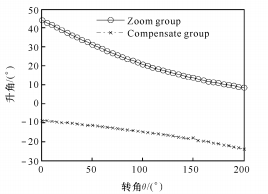
(a) Relación entre el ángulo de aumento de presión y el ángulo de rotación
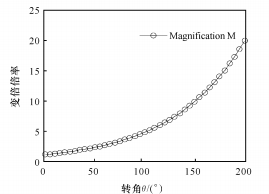
(b) Relación entre la relación de zoom y el ángulo de rotación
Fig. 4 Función de potencia entre θ y M
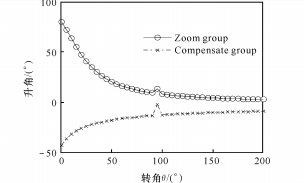
(a) Relación entre el ángulo de aumento de presión y el ángulo de rotación
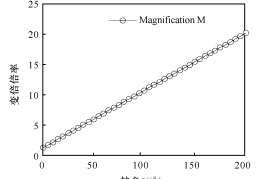
(b) Relación entre la relación de zoom y el ángulo de rotación
Fig. 5 Función exponencial entre θ y M
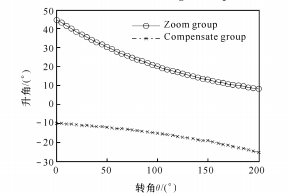
(a) Relación entre el ángulo de aumento de presión y el ángulo de rotación
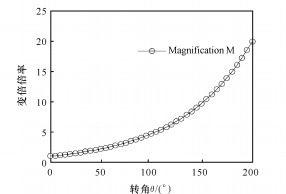
(b) Relación entre la relación de zoom y el ángulo de rotación
Fig. 6 Función logarítmica entre θ y M
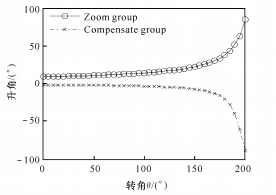
(a) Relación entre el ángulo de aumento de presión y el ángulo de rotación
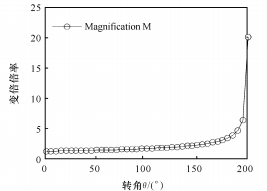
(b) Relación entre la relación de zoom y el ángulo de rotación
Fig. 7 Función de Gauss entre Q y M
El análisis del ejemplo anterior ilustra brevemente la influencia de diferentes valores del coeficiente de ajuste n en los resultados del diseño de la curva de leva, y la modificación adecuada de los parámetros puede obtener mejores resultados.
Durante la prueba, se descubrió que cuando n toma ciertos valores específicos, el ángulo de presión general de la curva de leva cumple con los requisitos y solo un cierto punto excede repentinamente un valor razonable. Este punto es lo que a menudo llamamos punto de inflexión de la curva, que es cuando la leva gira. Cuando alcanza cierto ángulo, de repente no puede seguir girando, es decir, queda atascado en la máquina.
Es fatal tanto para la estructura de la leva como para el efecto de zoom, por lo que al diseñar, debes evitar curvas con tales puntos de inflexión. Es decir, se requieren múltiples pruebas para garantizar que se obtenga un coeficiente de ajuste razonable.
Al mismo tiempo, si un cierto valor del coeficiente de ajuste puede optimizar la curva de la leva está relacionado con los requisitos del diámetro de la leva, el ángulo de presión de la curva de la leva que puede soportar y los requisitos del ángulo total de rotación de la leva. , el volumen y peso del sistema y los requisitos de velocidad del zoom.
Por lo tanto, el método de diseño para establecer la ecuación de la curva de leva de zoom del coeficiente de ajuste puede facilitar a los diseñadores modificar la curva de manera flexible, de modo que puedan cambiar la forma de la curva de leva de acuerdo con diferentes requisitos de diseño y encontrar la mejor curva de leva de zoom.
Saque aleatoriamente varias posiciones de zoom de los datos experimentales anteriores y llévelas al Código V para verificar que la superficie de la imagen sea estable y que la calidad de la imagen cumpla con los requisitos de diseño.
3. Resultados experimentales
De acuerdo con el análisis y la simulación anteriores, la leva de la lente con zoom que diseñamos se aplicó con éxito, como se muestra en la Figura 8. Después de la inspección de la fotografía de campo, la leva diseñada usando la teoría anterior en la lente con zoom tiene un zoom rápido, suave y preciso. curva de compensación, buena calidad de imagen en diferentes puntos focales y cumple plenamente con los indicadores de diseño, lo que verifica la exactitud del análisis anterior.

Figura 8 Lente de zoom
Seleccione la relación de función de potencia entre θ y M, y al cambiar el coeficiente de ajuste n, se pueden hacer diferentes compromisos entre la relación lineal entre θ y x y la relación lineal entre θ y m23, lo que no solo garantiza que el ángulo de aumento de presión no ser demasiado grande pero también evitar superar la grave falta de uniformidad en la velocidad de cambio de tasa.
Por supuesto, para obtener una relación lineal de θ-m23 o θ-dm23/dθ, puede aumentar el ángulo α o aumentar el diámetro del tambor de leva para reducir el ángulo máximo de aumento de presión de la curva de leva, pero esto aumentar el volumen y el peso de la lente. Disminuir la distancia focal del grupo de compensación también reducirá el ángulo máximo de aumento de presión de la curva de compensación.
Esto complicará la estructura del grupo fijo e incluso reducirá la calidad del diseño óptico. Por lo tanto, elegir la relación de la función de potencia entre θ y M puede ayudarnos a optimizar la curva de la leva y ayudarnos a diseñar una lente zoom miniaturizada de alta calidad.
Si desea obtener más información sobre la lente con zoom después de leer el contenido anterior, puede comunicarse con Quanhom para obtener una solución integral.
Como fabricante profesional deComponentes optoelectromecánicosCon muchos años de experiencia, Quanhom está equipado con un equipo profesional de I+D y un estricto sistema de inspección de calidad. Nuestras diversas lentes térmicas infrarrojas (LWIR,MWIRy cámaras SWIR) se venden en todo el mundo y han recibido elogios y la confianza de muchos clientes. Ponemos las necesidades de los clientes en primer lugar en todo y podemos brindarles servicios personalizados bien pensados. Si desea comprar nuestra lente de zoom continuo infrarrojo, ¡contáctenos de inmediato!
Autores: Yan Lei, Jia Ping, Hong Yongfeng, Wang Ping
Fuente de la revista: Vol.31 No.6 Journal of Applied Optics noviembre de 2010
Fecha de recepción: 2010-03-25 Fecha de revisión: 2010-6-23
Referencias:
[1] TANG Jian-bing. Diseño optimizado del contorno de la leva de enfoque variable [J]. Técnica óptica, 1994, 20(1) : 27-29. (en chino con resumen en inglés)
[2] ZHANG Xiu-li. Un nuevo método para mejorar el contorno de la leva de la lente de compensación [J]. Técnica Yunguang, 2003,35 (2): 16-17. (en chino con resumen en inglés)
[3] CUI Jun, SE Guo-Xiong. Diseño de ajuste del contorno de la leva del objetivo zoom [J]. Revista china de instrumentos científicos, 1990, 11 (1): 107-112. (en chino con resumen en inglés)
[4] Grupo de diseño de lentes de película. El diseño óptico del objetivo de fotografía de películas [M]. Beijing: Compañía Editorial de la Industria China, 1971. (en chino)
[5] CHANG Qun. Corpus de diseño óptico [M]. Beijing: Science Publishing Company, 1976. (en chino)
[6] CUI Ji-cheng. Diseño de lente zoom refractivo-reflectante de gran apertura [J]. Óptica e Ingeniería de Precisión, 2008? 16 (11): 2087-2091. (en chino con resumen en inglés)
[7] DONG Ke-yan, PAN Yu-long, WANG Xue-jin, et al. Diseño óptico de un sistema de zoom escalonado de doble banda infrarroja HDE [ J ]. Óptica e ingeniería de precisión, 2008,16 (5): 764-770. (en chino con resumen en inglés)
[8] HAO Hong-yun, Xiong Tao. Sistema óptico de campo de visión dual infrarrojo de longitud de onda media [J]. Óptica e Ingeniería de Precisión, 2008, 16 (10): 1891-1894. (en chino con resumen en inglés)
[9] CHEN Xin, FU Yue-gang. Diseño óptimo de curva de leva para sistema de zoom [J]. Revista de Óptica Aplicada. 2008, 29 (1): 45-47. (en chino con resumen en inglés)
[10] XU Zheng-Guang, ZHAO Yi-Fei, SONG Cai-Liang, et al. Optimización del diseño de curva de leva de zoom compuesto con OZSAD[J]. Revista de Óptica Aplicada, 2006,27 (3):203-207. (en chino con resumen en inglés)
[11] MENG Jun-he, ZHANG ZHen, SUN Xing-wen. Optimización de cámara de una lente con zoom [J]. Ingeniería de infrarrojos y láser, 2002, 31(1): 51-54. (en chino con resumen en inglés)
